Information Literacy in Mathematics Undergraduate Education: Where Does It Stand Today?

Jeffra Diane Bussmann
Senior Assistant Librarian
California State University, East Bay
Hayward, California
Jeffra.Bussmann@csueastbay.edu

Jeffrey D. Bond
Science Librarian
Texas Christian University
Fort Worth, Texas
j.bond@tcu.edu

Abstract

The published literature on information literacy in mathematics is relatively sparse. This article explores the current state of information literacy initiatives in undergraduate mathematics. The authors survey academic librarians (n=118) who liaise with mathematics departments in order to gain an understanding of their practices and attitudes towards this area.

Introduction

Information literacy (IL) instruction is a core function for most academic librarians who liaise with academic units and departments. Notable published research and case studies on IL instruction exists for a majority of the common college disciplines: art (performing, visual, music, etc.), biology, business, chemistry, engineering, English literature and composition, health sciences, psychology, sociology, and more (Lawal 2001; Christensen 2004; Larkin & Pines 2005; Ferrer-Vinent & Carello 2011; Peters 2011; Winterman et al. 2011; Fosmire 2012; Hoffmann & Adams 2012; Stanger 2012; Strittmatter 2012; Waters et al. 2012; Bandyopadhyay 2013; Loo 2013; Lyons & Warlick 2013; Bombaro 2014; Hess 2014; Knapp & Brower 2014; Zanin-Yost & Reitz 2014). IL instruction and related initiatives in mathematics appear rarely in the literature. Poster sessions and conversations at conferences are typically where mathematics IL initiatives are shared, but the shared knowledge and experiences seldom progress beyond the event. The primary purpose of this article is to begin the process of uncovering and sharing the perceptions and practices of librarians in relation to the IL needs of mathematics undergraduate students. In this article, the term 'math students' is used to refer to undergraduate students who are taking mathematics courses. "Math IL" is used to reference the IL framework, concepts and skills adapted and applied in the mathematics context.

Literature Review

Mathematics at the undergraduate level continues to be textbook focused, making it difficult to visualize where library use and IL instruction have a part in improving undergraduate student success. One of the earliest articles that explores this dynamic of library-related instruction for math students was written by Barringer in 1989. She states, "In taking mathematics beyond the textbook, so to speak, the library-related experience helps put the undergraduate's mathematics instruction into the broader liberal arts and sciences context" (p. 130).

Barringer provides details for several library assignments that can be integrated into math courses to introduce undergraduate students to mathematics information resources. She reasons that integrating assignments that require students to make use of mathematics information resources helps students to "gain an appreciation for the richness and variety of mathematics, and to foster a better understanding of the research processes and the development of the discipline" (p. 132). Barringer recommends that these library assignments be scaffolded in such a way that every mathematics major would complete all assignments before graduation. Barringer also concludes that library instruction in mathematics is an uncharted area ripe for new discoveries. This remains the case today, over 25 years later.

Writing a few years after Barringer, Hurlbert and Weida (1991) describe integrating library research into a sophomore mathematics foundations course. The course assignments were specifically designed to increase student involvement with both the writing center and the library. They revised the coursework to improve student success with higher-level writing skills and with a more comprehensive research practice. Even though the library experienced a noteworthy increase in mathematics book circulation, Hurlbert and Weida adjusted the assignment so that students were required to use a mixture of different source types. These instructors write that, "This research helps put [the students'] own struggles with mathematics in a new light and to change their concept of mathematics from a cold scientific subject to a more human struggle for understanding" (p. 194).

Anderson and Pausch's 1993 book focuses entirely on library service to the academic mathematics community. There is only a two-sentence paragraph that discusses library instruction for mathematics undergraduates, and one of those sentences is used to describe Barringer's program. In 1999, Leckie and Fullerton surveyed and interviewed science faculty, including mathematicians, about their perceptions of their students' information literacy skills and their support for and understanding of "bibliographic instruction," the term that was used at the time. The mathematics faculty responded that bibliographic instruction was not considered very important. They also indicated that library research was not needed for undergraduate mathematics coursework. Among science and engineering departments, mathematics faculty made the least use of the library-related instructional services.

Newby (2005) investigated mathematicians' use of online resources versus print. In this article, she highlights the differences in information use between mathematics and other science disciplines. Newby claims, "It is important that the math librarian collaborate with the faculty and graduate students who teach undergraduate math students to incorporate information literacy concepts into their syllabi so that undergraduates are better prepared to seek out and locate the appropriate mathematical literature, either online or in print" (p. 79). More recently, a case study by Spiegelman and Glass (2008) shares their successful collaboration as library faculty and mathematics faculty, respectively, to integrate IL instruction into a mathematics course at a community college. In particular, they incorporated Web 2.0 technologies and games to both enhance the course material and blend in IL outcomes.

Information technology has drastically changed the organization and use of information, including mathematical information sources and resources. Rutter (2002) in Notices of the American Mathematical Society, uses Ranganathan's Five Laws of Library Science to illustrate a picture of mathematicians and their unique relationship with libraries in a developing digital world. Within this context, Rutter stresses that searching for mathematics information is more complicated than it was only a few decades earlier. Now, another decade later, all the complexity she describes still exists: information continues to grow exponentially, the web is still chaotic and unstructured, and there remain multiple portals for access to online information. Rutter ends by asserting, "Because of the increasing complexity of the information environment and the growing requirement of specialized skills, scholars in mathematics need libraries and librarians today more than ever before" (p. 1081). How much she intended this 'need' to include math students is unclear.

Research Questions

The research questions that follow are designed to scan and uncover the information literacy instruction activities, practices, and perceptions of mathematics librarians for mathematics undergraduate students.

After consulting the literature and reflecting on the research goals, the authors developed three research questions to frame this study:

RQ1. Is mathematics information literacy being taught at colleges and universities by librarians for mathematics undergraduate students?

RQ2. In what ways is mathematics information literacy being taught to mathematics undergraduates?

RQ3. What are the factors that affect the inclusion of mathematics information literacy initiatives for mathematics undergraduates at colleges and universities?

Methods

Fosmire's (2000) physics-based library instruction survey was used as a starting point for the survey because many of its questions correspond with the research interests in this study. Basic revisions to the survey content were necessitated by information technology advances. It was important to keep the three research questions in mind during the editing process in order to ensure that each survey question remained in scope. Once the initial draft of the survey was complete, four science and instruction librarians were recruited to review it for constructive feedback. With this feedback and after attending an Association of College and Research Libraries (ACRL) Science and Technology Section (STS) chat session that focused on math IL instruction, further revisions were made and finalized in Qualtrics. In order to provide an opportunity to extend the research beyond the quantitative approach, the survey included a final question inviting respondents to participate in follow-up interviews, where more in-depth questions could be posed. The survey instrument is provided in Appendix A.

The research was focused geographically on instruction in the United States and Canada. E-mails containing invitations to the survey were distributed to four relevant librarian e-mail distribution lists: ILI-L (e-mail list for the Instruction Section of ACRL), PAMNET (the e-mail list for the Special Libraries Association Physics, Astronomy and Mathematics division), SciTech (the e-mail list for the SLA Science-Technology division), and STS-L (the e-mail list for ACRL-STS). Furthermore, the recruitment e-mail specified that only librarians who liaise with the mathematics departments should complete survey.

Results

A total of 121 persons responded to the survey. Seven respondents were from Canada, and 111 were from the United States. The responses outside the geographical scope were disregarded, leaving 118 usable survey responses. Below is a summary of the relevant and meaningful results. The complete anonymized quantitative result details are provided in Appendix B.

Demographics

The survey asked respondents to indicate their length of experience working with mathematics and mathematicians (Table 1). The plurality of respondents indicated fewer than two years of experience working with mathematics (36.4%). The median of responses was in the 2-5 year range.

Table 1. How long have you been a librarian who liaisons with mathematics/mathematicians?

Years	Number of respondents
Less than 2 years	36
2-5 years	16
6-10 years	16
11-15 years	12
16-25 years	11
25+ years	8

Respondents also answered a question regarding their personal degree attainment in the field of mathematics. Only 5.8% of respondents reported having a mathematics degree at a masters level or higher. Close to one quarter (24.3%) reported having a mathematics degree at a bachelors level or higher.

Institutional Profiles

The survey asked several questions about the respondents' institutions. Because there is no way of knowing the exact institutional affiliation of respondents, it is possible that some institutions could be represented more than once in these statistics, though not likely because it is rare for an institution to have more than one librarian responsible for mathematics.

In response to a question about the academic degrees offered at their institutions, 40.6% of respondents indicated that a mathematics PhD is offered. On the opposite end, 9.3% of respondents indicated that no mathematics degree of any kind is offered.

Respondents answered a question regarding the overall FTE enrollment at their institutions (Table 2). Exactly one quarter of respondents work at institutions that have enrollments exceeding 25,000 students. Respondents also answered a similar question about the number of undergraduate mathematics majors at their institution (Table 3). Of the respondents, 34.1% indicated a count of more than 100 mathematics majors.

Table 2. How many total students does your institution enroll (FTEs)?

FTE	Number of respondents
1-1,000	4
1,001-5,000	32
5,001-10,000	18
10,001-25,000	37
25,001+	27

 

Table 3. How many undergraduate mathematics majors [are enrolled your institution]?

Math majors	Number of respondents
None	9
1-10	4
11-50	34
51-100	25
101-250	22
251+	12

IL Instruction Questions

In the survey, there were three IL-related questions that all survey participants were asked. The first determined if the participants' institution has a systematic plan or program for IL instruction that would include all students of a certain group, i.e. all freshmen, all science majors, all mathematics majors. Respondents could select all options that apply, and there were a few respondents who selected more than one. Nearly half of the respondents (46.4%) said all students must take a class that includes an IL component. Only seven respondents (6.1%) answered that their students are required to take a stand-alone IL course as a part of their degree program. Nine respondents affirmed that all science majors must take a course that includes an IL component. Surprisingly, seven respondents indicated that all mathematics majors must take a course that includes an IL component. Nearly 40% of the respondents said their institution does not have a systematic program, curriculum plan or procedures in place for IL instruction. In the "Other" section, several respondents mentioned first-year programs that include a mandatory IL component. Additional respondents remarked that their institution had no mandatory IL component. Because of the high similarity of some of the "Other" responses to the pre-existing response options, the authors recognize that this question may lack clarity. Also shared were statements that discussed IL being integrated into classes across the disciplines. One librarian mentions a math course that includes IL but "only sporadically."

The second question elicited whether or not the respondents had taught any IL sessions for specific mathematics courses, programs, or activities between Fall 2010 and Summer 2014. Out of the 116 respondents who answered this question, only 35 (30.2%) answered affirmatively. Therefore, over two-thirds of the respondents have not taught an IL or library-related session to math students during that four-year time period.

Using a Likert scale from strongly agree to strongly disagree, all respondents were asked to evaluate the statement: "The information literacy needs of mathematics undergraduate students are being adequately met at my institution." Zero respondents selected that they "Strongly" agreed with this statement. Only seven respondents (6.4%) agreed that the IL needs of math majors are being met. Forty-six (42.2%) selected the 'Neutral' response. Altogether 56 respondents (51.4%) chose "Disagree" or "Strongly disagree" and therefore, indicated that they perceive that the IL needs of math students are not being adequately met. While there was no space within this question for comments, a few respondents provided related feedback in the final 'Additional Comments' question of the survey. For example, one respondent said, "Information literacy for mathematics major seems premature." Remarks in this section also suggest that confusion and uncertainty over the definition of math IL caused some respondents to select Neutral. In particular, one respondent commented, "For undergraduate math students, it is less clear that they have specific information needs in mathematics. They *do* have unmet information needs. But it is unclear what this institution will do about that. So the question about whether the institution I work at serves the information needs of mathematics students struck me as unclear. As a result I answered 'neutral.'"

IL Session Details

Another set of survey questions were given to those 35 respondents who answered positively to teaching an IL session in the Fall 2010 to Summer 2014 time period. After the first question in the set, respondents were invited to check all responses that applied. This first survey question asked for the number of sessions they taught during each of those academic years. A majority of the respondents indicated that they taught either zero or one session per academic year (Fig. 1). Thus, even among this smaller subset of respondents, one quarter still did not teach an IL session in any particular year. There are a few impressive cases where respondents taught more than five sessions per academic year. Respondents who were not liaising to mathematics and/or not at the same institution in any one of the academic years covered could choose the 'N/A' option.

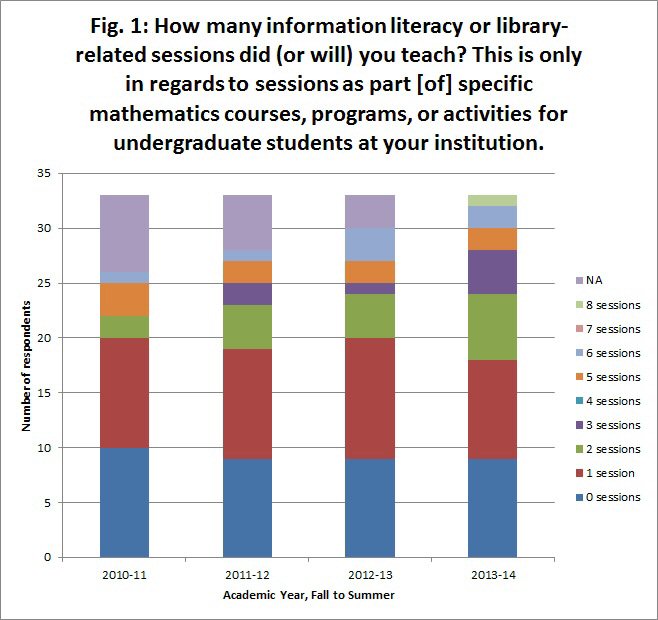
Figure 1

The next question asked in which mathematics courses these IL sessions were taught, listing four courses commonly associated with IL sessions. Respondents could name additional courses by using the 'Other' option. Tied for most responses with nine respondents (29.0%) were the mathematics history course and the required seminar series for mathematics majors. The mathematics education course followed with six respondents (19.4%), and the mathematics literature research course was selected by four respondents (12.9%). The 'Other' option had 11 respondents, several of whom mentioned statistics, and a few other courses including: a seminar on code-breaking, the mathematics of gaming, and a mathematics of democracy course.

Also of interest was the delivery method the librarians used in their IL sessions. In Figure 2, in-person demonstration was the most frequently used method with selection by 30 respondents (96.8%). Online subject-based guide (58.1%) and hands-on time or interactive session (54.8%) were the next most frequently incorporated instruction method. Course guides (41.9%) and paper handouts (35.5%) are also still used regularly by librarians. The 'Other' section did not receive any responses. The results demonstrated that the most typical delivery method for math IL instruction is in-person, of which more than half of these librarians also use an online subject guide and incorporate a hands-on, interactive session.

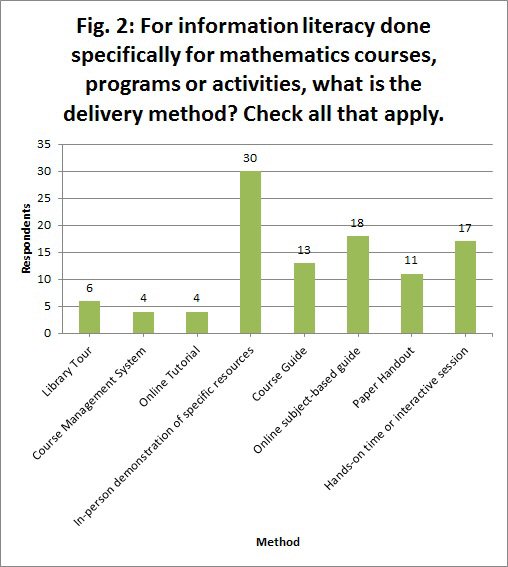
Figure 2

Respondents were then asked which mathematics-related information resources math students are expected to use (Fig. 3). Journals and monographs tied for first place with the most responses (74.2%), followed by OPAC/library catalog (58.1%). MathSciNet/Mathematical Reviews database (54.8%) came in a close third. The choice "Web of Science, Compendex, and/or other databases" was selected by 45.2% of the respondents. All other resources were below 40% expected use. One respondent did mention Wikipedia in the 'Other' category and two more selected the "I don't know" option.

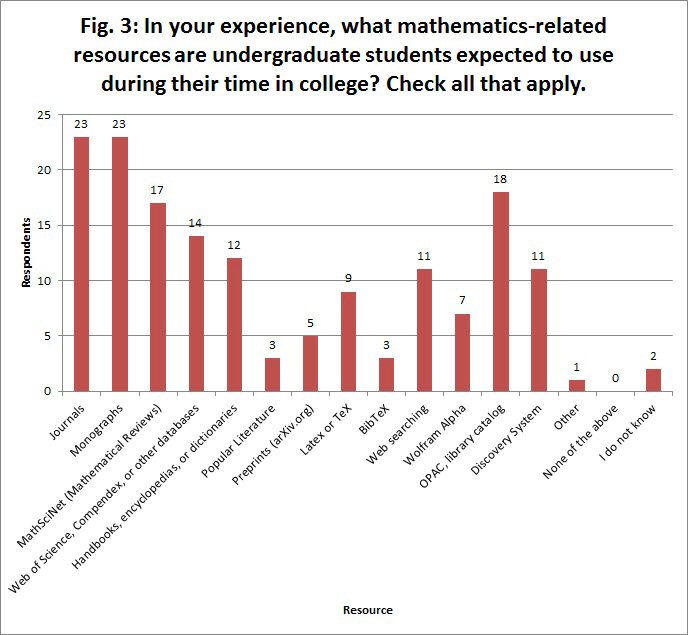
Figure 3

Additionally, librarians were asked to reflect on these IL instructional experiences and select all the kinds of assignments they encountered that require mathematics students to use skills and/or knowledge acquired in an IL session. The most frequently selected assignment was the paper (58.1%). A research/honors project was next (48.4%), followed closely by senior project/thesis or culminating experience (45.2%). Presentation and group/team work were both selected by 11 respondents (35.5%). Only 8 respondents (25.8%) encountered posters as assignments that require skills and/or knowledge from an IL session. One respondent selected 'None of the above,' and another wrote in "I don't know."

The last question of the set asked about the competencies that librarians address in their IL sessions with math students (Fig. 4). The top selected competency with 25 respondents (83.3%) was "How to search/use mathematics-related resources (such as MathSciNet)." Coming in at a low second was "Which journals are particularly important," selected by 10 respondents (33.3%). Seven respondents (23.3%) taught about the standard structure of a mathematics journal. Response rates for the other listed competencies were under 20%. Notably, no respondent selected the competency for writing and/or submitting a journal article. One 'Other' answer included how to use LaTeX and BibTeX; another mentioned identifying differences between popular and scholarly articles. A respondent also pointed out using other "non-math databases" to find "statistics-rich studies."

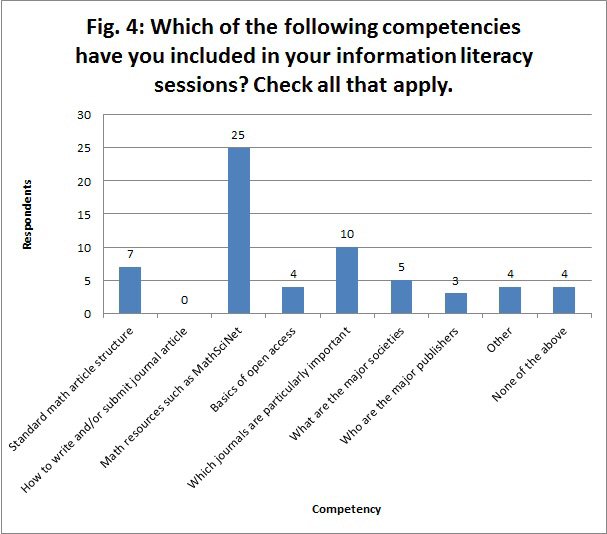
Figure 4

Additional Comments

The IL content portion of the survey ended with an open-ended request: "Please take a moment to make any additional comments about your answers on this survey, or about mathematics information literacy in general." Nearly half the respondents who contributed additional comments reported issues with mathematics instructors who were in some way resistant to bringing IL instruction to math students. Similarly, nearly half of the respondents also mentioned concerns regarding the actual IL needs of math students. More than half of the comments contained negative wording on IL initiatives for math students (i.e., tough sell, resistant, hardest department). Several respondents used this section to provide additional details on their instructional sessions. A few expressed interest in developing math IL initiatives at their institutions. Appendix C contains respondents' statements that represent these themes. While these comments are intriguing and insightful, there is potential for a more thoughtful analysis of them in conjunction with a forthcoming qualitative component of the research study. The authors plan to conduct follow-up interviews with those respondents who volunteered to participate in this second portion of the study. Also, the authors intend to gather answers to the more complex RQ3.

Analysis and Discussion of the Survey Results

The most striking result of the survey was the very clear answer to RQ1: the strong majority of librarians surveyed are not teaching IL to mathematics undergraduate students. This response supports the perception gathered from the literature review and informal conversations that math is a discipline that rarely incorporates IL instruction into its curriculum.

Research Question 2 addresses methods of teaching math IL. Survey results indicate math IL is most frequently taught through a math history course or a required seminar for math majors. The math history course fits the parameters for IL inclusion because of its potential for students to do a bibliography report, a literature review, or research paper on a particular math topic or math historical figure. While the course content for a required seminar can vary significantly by institution, frequently it is meant to enrich math students' exploration of math and its potential for research and application. Including IL in this course helps math students gain an appreciation for math resources beyond the textbook.

When designing an IL session, a librarian should know the students' information needs as well as the math professor's expectations, including the details of assignments and projects. In teaching their IL sessions, librarians see journals and monographs as the information resource most likely to be used. Math has traditionally been recognized as seeing greater value in books than other science disciplines; therefore, it makes sense that math professors might expect their students to make use of math books (Anderson & Pausch 1993). Tying IL sessions to a particular assignment or project makes the session immediately relevant to the students. Papers, research projects, and senior projects are the most frequently assigned work encountered by librarians. In the humanities and social sciences, assignments and projects that require in-depth information research are a core part of undergraduate degree attainment; however, they are less frequently required in the sciences (Scaramozzino 2010). While it is clear that a majority of the surveyed librarians focus on search strategies and resource types, a few did incorporate other IL facets, such as the process by which scholarly information is made and shared and the evaluation of authority in the field.

Uncovering an answer to RQ3 proved to be more complex than anticipated. The authors performed a statistical analysis to discern deeper relationships among the responses that would in turn highlight potential factors of influence. The statistical analysis of the survey data is limited because distributing the survey via large and overlapping e-mail lists means that a response rate cannot be calculated. Given this limitation and the goal to find connections among the respondents' selections, the chi square test for independence was performed using pairs of survey questions. The first survey question to be paired was the question on whether any IL classes had been taught in the last four years. This question was paired with each of the institutional and respondent demographic questions. Then, the survey question regarding whether the IL needs were being met at the respondent's institution was paired with the same demographic questions. Finally, the two above IL survey questions were paired with each other. The full list of chi-square tests and respective p-values are included in Appendix D.

In only one pairing is the p-value below 0.05. This was for the pairing of questions concerning whether IL needs are being met at the respondent's institution and the question about total size of the institution. A careful review of the contingency table, however, gives no clear guidance that answers any research questions. Ultimately, there were no significant relationships discovered in this statistical analysis, and, therefore, no strong claims can be made about factors that influence the inclusion of math IL instruction (RQ3).

Conclusion and Future Research

Very few librarians who liaise with mathematics departments are conducting IL instruction sessions for mathematics undergraduate students. Those few librarians who teach IL to math students do so through expected courses such as the history of math and required research seminars, and through unusual courses such as code-breaking and mathematics and democracy. They incorporate a mixture of methods, tools, and IL competencies to help students accomplish a variety of assignments. Most frequently, librarians in the survey used in-person demonstrations to teach the effective use of and searching techniques in MathSciNet and the library catalog. The factors that cause or influence the integration of IL instruction by librarians into math courses, programs, or activities are not yet identified. The answer to this research question will be pursued during the qualitative study.

Returning to the question inspired by Rutter (2002), is IL instruction necessary for math students in the specific context of mathematics? Future research could explore and assess the relationship between IL instruction and math students' ability to meet student or program learning outcomes with a comparison between students who receive math IL instruction and those who do not. If an institution or math degree program requires its undergraduate students to complete a senior project or culminating experience for graduation, student work such as bibliographies and reference lists could be examined for source quality, quantity and variety. Alternatively, math faculty could be surveyed to determine their perception of math IL in regards to undergraduate students and their preparation for dealing with information beyond the textbook and classroom. It would be useful to also include a question that inquires if they incorporate instruction or assignments that require math students to make use of IL knowledge, skills or concepts.

As stated previously, math has traditionally been a low user of IL instruction. The results from this 2014 survey indicate IL instruction for math students is still rare today. With the new IL framework being formalized by ACRL, will this create a new opening for math librarians to engage math faculty and undergraduate students? Do the framework and the threshold concepts have more obvious applicability for mathematical sciences in undergraduate education? Research and reflection could be conducted to consider how this new IL framework fits into the mathematical academic world.

References

Anderson, N.D. & Pausch, L.M. 1993. A Guide to Library Service in Mathematics: The Non-Trivial Mathematics Librarian. Greenwich, CT: JAI Press.

Bandyopadhyay, A. 2013. Measuring the disparities between biology undergraduates' perceptions and their actual knowledge of scientific literature with clickers. Journal of Academic Librarianship 39:194-201.

Barringer, S.H. 1989. Introducing undergraduates to mathematics information resources. Research Strategies 7:129-133.

Bombaro, C. 2014. Overcoming the barriers to information literacy programs: CALM Lab for English majors at Dickinson College. Reference Services Review 42:24-262.

Christensen, B. 2004. Warp, weft, and waffle: Weaving information literacy into an undergraduate music curriculum. Notes 60:616-631.

Ferrer-Vinent, I.J. & Carello, C.A. 2011. The lasting value of an embedded, first-year, biology library instruction program. Science & Technology Libraries 30:254-266.

Fosmire, M. 2000. Bibliographic instruction in physics libraries: A survey of current practice and tips for marketing BI. Science & Technology Libraries 19:25-34.

Fosmire, M. 2012. Information literacy and engineering design: Developing an integrated conceptual model. IFLA Journal 38:47-52.

Hess, A.N. 2014. Online and face-to-face library instruction: assessing the impact on upper-level sociology undergraduates. Behavioral & Social Sciences Librarian 33:132-147.

Hoffmann, D. & Adams, V. 2012. Faculty/librarian collaboration: A faculty perspective on information literacy instruction. Codex 2:25-35.

Hurlbert, J.M. & Weida, R.A. 1991. Developing a BI project for mathematics research in the small college library. Research Strategies 9:189-94.

Knapp, M. & Brower, S. 2014. The ACRL Framework for Information Literacy in Higher Education: Implications for health sciences librarianship. Medical Reference Services Quarterly 33:460-468.

Larkin, J.E. & Pines, H.A. 2005. Developing information literacy and research skills in introductory psychology: A case study. Journal of Academic Librarianship 31:40-45.

Lawal, I.O. 2001. Integrating chemical information into the undergraduate curriculum. Science & Technology Libraries 20:43-57.

Leckie, G.J. & Fullerton, A. 1999. Information literacy in science and engineering undergraduate education: Faculty attitudes and pedagogical practices. College & Research Libraries 60:9-29.

Loo, J.L. 2013. Guided and team-based learning for chemical information literacy. Journal of Academic Librarianship 39:252-259.

Lyons, T. & Warlick, S. 2013. Health sciences information literacy in CMS environments: learning from our peers. Electronic Library 31:770-780.

Newby, J. 2005. An emerging picture of mathematicians' use of electronic resources. Science & Technology Libraries 25:65-85.

Peters, M.C. 2011. Beyond Google: Integrating chemical information into the undergraduate chemistry and biochemistry curriculum. Science & Technology Libraries 30:80-88.

Rutter, S. 2002. Mathematicians and the mathematics library: A librarian's perspective. Notices of the American Mathematical Society 49:1078-1081.

Scaramozzino, J.M. 2010. Integrating STEM information competencies into an undergraduate curriculum. Journal of Library Administration 50:315-333.

Spiegelman, M. & Glass, R. 2008. Gaming and learning: Winning information literacy collaboration. College & Research Libraries News 69:522-547.

Stanger, K. 2012. Whose hands ply the strands? Survey of Eastern Michigan University psychology faculty regarding faculty and librarian roles in nurturing psychology information literacy. Behavioral & Social Sciences Librarian 31:112-127.

Strittmatter, C. 2012. Developing and assessing a library instruction module for a core business class. Journal of Business & Finance Librarianship 17:95-105.

Waters, N., Kasuto, E. & McNaughton, F. 2012. Partnership between engineering libraries: Identifying information literacy skills for a successful transition from student to professional. Science & Technology Libraries 31:124-132.

Winterman, B., Donovan, C. & Slough, R. 2011. Information literacy for multiple disciplines. Communications in Information Literacy 5:38-54.

Zanin-Yost, A. & Reitz, C.L. 2014. Information literacy in music history: Fostering success in teaching and learning. Journal of Library Administration 54:562-572.

Appendix

Appendix A. The Survey Instrument [PDF]

Appendix B. Quantitative Results of the Survey [PDF]

Appendix C. Quotes from Survey Respondents in the Additional Comments Section [PDF]

Appendix D. Chi-Square Tests Run on Survey Questions [PDF]

Previous

Contents

Next

This work is licensed under a Creative Commons Attribution 4.0 International License.